Geometry in an Analog Clock
Mar 15, 2023
Learning to program a computer forces us to look differently at the world around us. Take an analog clock, for example. On the surface, we might see a circular face with numbers representing the hours. There might be tick marks representing minutes, and there are two or three hands of varying thicknesses and lengths that indicate the current time.
Draw Me a Clock
Consider now how you would write a precise set of instructions that explain to someone how to draw such a clock. As challenging as this might be with another person, it is far more difficult to write the instructions for a computer since it has no previous experience from which to draw. Where you might tell a person, "Write the numbers 1 through 12 in order around the outer edge of the circle so that they are evenly spaced and so that the 12 is at the top," a computer would need much more information. With the computer, you almost need to start with first principles.
Add a Dash of Geometry
The xy-coordinate plane from geometry is a way to precisely locate points relative to a fixed position called the origin. If we overlay a coordinate plane onto the face of the clock with the origin in the center, then we are able to use (x,y) coordinates to locate any point on the face.

Many programming languages either include commands for drawing two-dimensional (2D) shapes or have libraries that add this capability. For example, the 2D graphics context used with the HTML5 <canvas> element has an arc function that can be used to draw a circle representing the face.
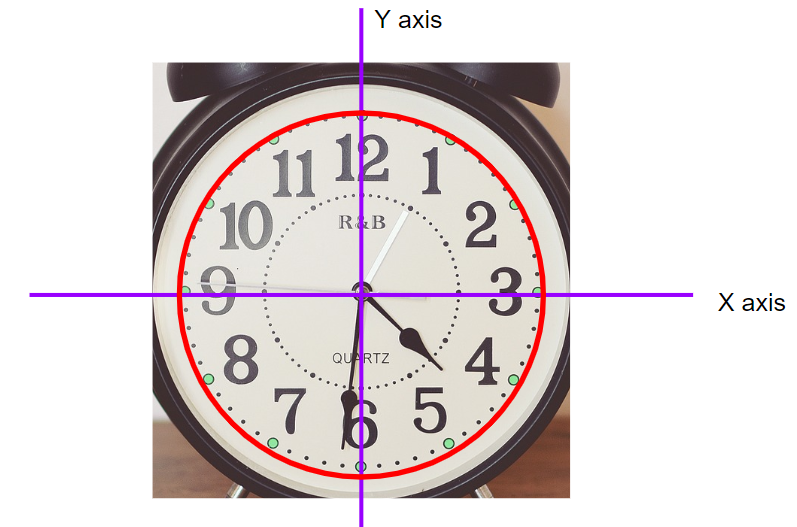
Every point on the circle is a given distance from the center and at a particular angle with either the x- or the y-axis. The angle with the y-axis is easier to calculate in this context, because it represents the portion of a 24-hour day or the number of minutes in an hour. For example, "2" on the face of the clock is either 2 of 12 hours or 10 of 60 minutes. Both of these fractions reduce to 1/6. Since a circle contains 360 degrees, we know that "2" is 60 degrees from the y-axis.

However, our lives would be easier (for reasons I'll explain in a moment) if we knew the angle from the x-axis instead. Since the x- and y-axes form a right angle, the angle formed with the x-axis is the complement of the angle formed with the y-axis. In other words, these angles must add to 90 degrees. Therefore, "2" is 30 degrees from the x-axis.
Throw in a Splash of Trigonometry
Why does it help to know the angle formed with the x-axis? For that, we need just a bit of trigonometry. In trig, the base and height of a right triangle can be calculated if we know the length of the hypotenuse and the angle between the hypotenuse and the base.

With these ratios, we now have everything we need to draw numbers around the face of the clock or any of the hands needed to tell the time!
There is one more caveat, though. Some programming languages and libraries use radians instead of degrees for drawing arcs or working with trig functions. Therefore, we might have to convert our angle from degrees to radians. Fortunately, this is easy. There are 2𝛑 radians (yes, that's pi!) in 360 degrees. That means 180 degrees is 𝛑 radians, so 1 degree is 𝛑/180 radians.

Who Said I'll Never Use This!
There's math like this hiding in plain sight in things we use everyday. We often take it for granted because understanding the math isn't necessary to use the object effectively. Most of us can read the time from an analog clock without worrying about angles, radians, and trig ratios. However, programmers and engineers do need to understand the inner workings of things like clocks, and they often use math to describe or explain them. Used this way, math is a practical tool and a precise language for saying exactly what you mean!
Just a Bit of Code
In case you're curious, the JavaScript code to do the math outlined above to calculate the end point for the minute hand is:
angle = 90 - (minutes / 60) * 360;
radians = angle * Math.PI / 180;
x = Math.cos(radians) * minuteHandLength;
y = Math.sin(radians) * minuteHandLength;
The x and y variables could then be used with a lineTo command to draw a segment from the origin:
context.beginPath(); context.moveTo(center.x, center.y); context.lineTo(center.x + x, center.y - y); context.stroke();
Here, context is the graphics context for an HTML5 <canvas> element, and the center's x and y coordinates are half the width and height, respectively, of the canvas.
Want more code? There's a complete project in our Library that walks students through creating a web application that shows both an analog and a digital clock inside a web browser!
Stay connected with news and updates!
Join our mailing list to receive the latest news and updates from our team.
Don't worry, your information will not be shared.
We hate SPAM. We will never sell your information, for any reason.

